The primary purpose of the initialization vector IV is to act as a nonce. As a result, it must be distinct for every authenticated encryption operation under the same key. As long as distinctiveness can be guaranteed, the IV can be randomly generated. Moreover, the IV is included in the GCM encryption and authentication process so that it is not necessary to add it to the additional authenticated data A.

GCM authenticated encryption is shown in Algorithm 6. The output of the operation consists of a ciphertext C and an authentication tag T. The authentication tag applies to the plaintext P and the additional authenticated data A.

  Algorithm 6: GCM authenticated encryption operation.

Require: Shared key k, initialization vector IV , plaintext P, additional authenticated data A
 Ensure: Ciphertext C, authentication tag T
 H ← ek(0128)
 if len(IV ) = 96 then
 Y 0 ← IV  ∥ 031 ∥ 1
 else
 Y 0 ← GHASH(H,{},IV )
 end if
 for i = 1 … n do
 Y i ← Y i−1 + 1 if i < n then
 Ci ← Pi ⊕ ek(Y i)
 else
 Cn ← Pn ⊕ MSBu(ek(Y n))
 end if
 T ← MSBt(GHASH(H,A,C) ⊕ ek(Y 0))
 return C,T

The security strength of the authentication is determined by the desired length of the authentication tag. If plaintext P is empty, GCM acts as a MAC algorithm for the additional authenticated data A. This GCM mode is called GMAC.

The GCM authenticated decryption operation takes the following five inputs:

• The shared secret key k
• The initialization vector IV
• The ciphertext C
• The additional authenticated data A
• The received authentication tag T

Algorithm 7 shows how GCM authenticated decryption is computed. Recall that the IV used in the decryption process must be the same as was used in the encryption process.

The output of the decryption operation is either the plaintext message P or a special symbol ⊥ indicating that the integrity and authenticity verification of the received message failed; that is, the received tag and the computed tag did not match. Symbol ⊥ is referred to as FAIL in the GCM standard [57].

  Algorithm 7: GCM authenticated decryption operation.

Require: Shared key k, initialization vector IV , ciphertext C, additional authenticated data A, received authentication tag T
 Ensure: Plaintext P or symbol ⊥
 H ← ek(0128)
 if len(IV ) = 96 then
 Y 0 ← IV  ∥ 031 ∥ 1
 else
 Y 0 ← GHASH(H,{},IV )
 end if
 T´← MSBt(GHASH(H,A,C) ⊕ ek(Y 0))
 for i = 1 … n do
 Y i ← Y i−1 + 1
 if i < n then
 Ci ← Pi ⊕ ek(Y i)
 else
 Cn ← Pn ⊕ MSBu(ek(Y n))
 end if
 end for
 if T = T´ then
 return P
 else
 return ⊥
 else

Choosing ⊥ as the output symbol in case of an authentication failure nicely illustrates the concept of secure defaults. The decrypting party can rely on GCM to output a symbol that, if the message authentication failed, cannot be confused with valid plaintext. In other words, whenever GCM returns plaintext, the message integrity and authenticity of that message are guaranteed and the decrypting party does not need to perform any additional checks.

Figure 16.1 shows a diagram of the AES-GCM mode applied to one block of associated data A1 and two blocks of plaintext P1,P2. The symbol ⊗H denotes polynomial multiplication by the hash key H, the authentication key derived from the secret key K. The AES-GCM mode uses a variant of the counter mode (CTR) for encryption.

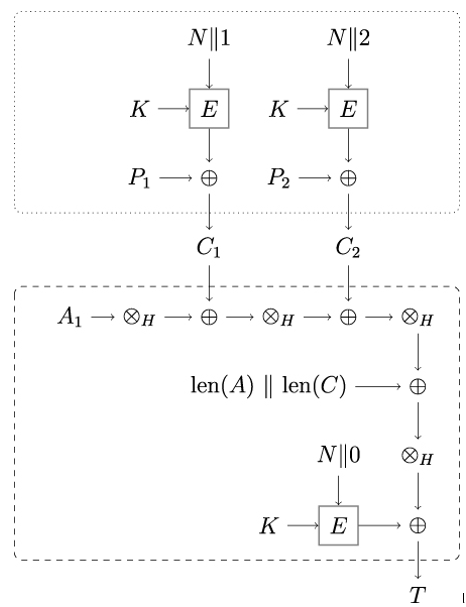
Figure 16.1: Illustration of AES-GCM mode

The operations within the dotted rectangle at the top of Figure 16.1 are nothing but the Counter (CTR) mode of a block cipher. The AES encryption operation denoted by E takes the secret key K and the nonce N concatenated with a counter to produce 128-bit blocks of the key stream that is XOR’ed with the plaintext blocks P1,P2, correspondingly. The obtained ciphertext blocks are denoted as C1,C2.

The operations within the dashed rectangle at the bottom of Figure 16.1 correspond to the GHASH function. GHASH takes the associated data A1 and performs a series of polynomial multiplications ⊗H and XOR operations ⊕ with the hash key H and the ciphertext blocks C1,C2. It then takes the result and XORs it with the term len(A) ∥ len(C), which corresponds to the bit length of the associated data A and the bit length of the ciphertext C, respectively.

Finally, the authentication tag T is computed as T = GHASH(H,A,C) ⊕EK(N∥0), where EK is the AES encryption under the secret key K. The hash key H is computed as H = EK(0), that is, the encryption of the block consisting of a sequence of 0x0 bytes (this step is not shown in Figure 16.1).