It is easy to show that even given a probabilistic public-key encryption scheme like the one defined above – that is, a scheme offering semantic security against any polynomial time adversary – Mallory can construct a new ciphertext c′, which corresponds to the complement of Alice’s plaintext. To do this, Mallory simply takes Alice’s ciphertext

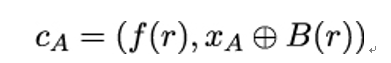
and modifies it to obtain

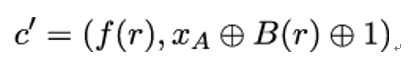
When Trent afterward decrypts the spoofed ciphertext c′ instead of Bob’s original ciphertext cB, he obtains:

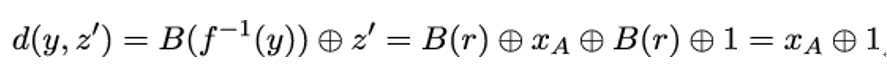
instead of the plaintext actually transmitted by Bob:

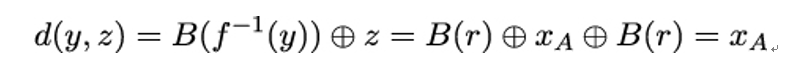
As a result, by replacing Bob’s ciphertext cB with c′, Mallory can force Trent’s XOR operation to yield a 1 even though she has no idea whether Alice’s bit xA had the value 0 or 1:

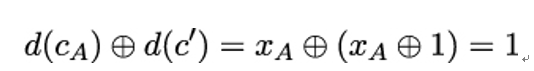
The example demonstrates that in some cases indistinguishability is not sufficient. In addition, the encryption scheme must be non-malleable: if Mallory is given some ciphertext c, it must be computationally infeasible for him to construct a different ciphertext c so that the corresponding plaintexts m and m have some known relationship [117].

In formal terms, the notion of non-malleability can be expressed using the following game with encryption oracle Owen and decryption oracle Oscar:

1. Owen generates a random secret key k.
2. Mallory can ask Owen to compute ciphertexts for an arbitrary number of plaintexts of her choice. In addition, Mallory can ask Oscar to decrypt a set of ciphertexts of her choice, but she can only ask Oscar once.
3. Mallory chooses a pair of equal-length messages m0,m1.
4. Next – if Mallory has not yet queried the decryption oracle Oscar – Owen chooses a bit b ← {0,1} at random, computes the challenge ciphertext c = ek(mb), adds c to the set of ciphertexts 𝒞, and returns c to Mallory.
5. Upon receiving c, Mallory continues to have oracle access to Owen and to Oscar. When Mallory queries Oscar with a set of ciphertexts, Oscar returns the corresponding plaintexts, except for ciphertexts in 𝒞. In addition, once Mallory asks Oscar to decrypt a set of ciphertexts, Owen will not compute new challenge ciphertexts.
6. Finally, Mallory must guess whether bit b was 0 or 1. If Mallory’s guess is correct, we say that she succeeds.

We say that secret key encryption is non-malleable under a chosen-ciphertext attack or, simply, NM-CPA, if Mallory succeeds in the above game with a probability p that is at most negligibly greater than 1 ∕ 2:

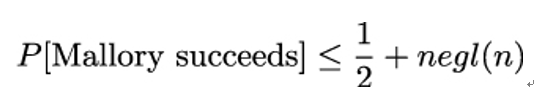
You might wonder how the above game describes non-malleability without modeling an attacker who alters a ciphertext in some specific way. The reason behind this is that in 2006, the Indian cryptographer Mihir Bellare and the American cryptographer Amit Sahai proved that non-malleability is equivalent to so-called indistinguishability under a parallel chosen ciphertext attack where Mallory’s queries to the decryption oracle may not depend on the answers to previous queries and must be made all at once [19]. This is exactly the attack that the above game describes.

The next two cryptographic concepts bring us even closer toward our goal of providing confidentiality and authenticity at the same time.