15.1.2 Indistinguishability under a chosen-ciphertext attack

Chosen-Ciphertext Attack (CCA) is a more powerful attack than a chosen-plaintext attack. Recall that in a chosen-plaintext attack Eve is able to encrypt plaintexts of her choice. In a CCA setting, Eve additionally is allowed to decrypt ciphertexts of her choice [97]. This ability is formalized by saying that Eve has access to a decryption oracle, say, Oscar.

Similar to CPA-security, the formal definition of CCA-security is captured in the following game:

1. Owen or Oscar generates a random secret key k.
2. Eve can ask Owen to compute the ciphertexts for any plaintexts of her choice. Also, she can ask Oscar to compute the plaintexts for any ciphertexts of her choice.
3. Eve then chooses a pair of equal-length messages m0,m1.
4. Next, Owen chooses a bit b ← {0,1} at random and computes the challenge ciphertext c = ek(mb).
5. Upon receiving c, Eve continues to have oracle access to Owen and Oscar, but she is not allowed to ask Oscar for the decryption of the challenge ciphertext c.
6. Finally, Eve must guess whether bit b was 0 or 1. If Eve’s guess is correct, we say that Eve succeeds.

A secret key encryption is said to have indistinguishable encryptions under a chosen-ciphertext attack, also referred to as IND-CCA or CCA-secure, if Eve succeeds in the above game with a probability p that is at most negligibly greater than 1 ∕ 2:

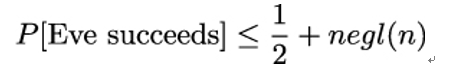
If, after some extensive interaction with Oscar, Eve finds a way to manipulate ciphertexts and to predict the consequences of these manipulations for the corresponding plaintexts, she can win this game. Therefore, CCA-security implies another very important property of secret key encryption schemes called non-malleability.

15.1.3 Non-malleability under a chosen-plaintext attack

The notion of non-malleability is somewhat more involved. We will first try to get an intuitive understanding of why non-malleability is important using a simple example, and then give a formal definition using the game notation equivalent to those for IND-CPA and IND-CCA.

Informally, an encryption scheme is said to be non-malleable if, upon observing ciphertext c = ek(m), Mallory cannot generate a different ciphertext c′ that decrypts to a value m′ somehow related to m.

A famous example of a malleable cipher is provided by the RSA encryption algorithm. Recall from Chapter 7, Public-Key Cryptography, that if Alice has the public key PKAlice = (e,n), a message m is encrypted to

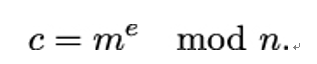
Taking c′ to be

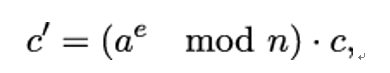
we see that

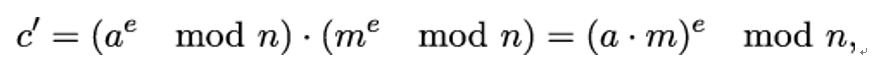
so the corresponding plaintext is m′ = am.

More generally, in the computational security setting we are currently in, saying that Mallory cannot generate such a c′ means that there exists no polynomial time algorithm able to do this. Moreover, requiring m′ to be somehow related to m means that there must be a relation R(m,m′) between m and m′ that can be computed in polynomial time.