15.2.2 MAC-then-encrypt

The MAC-then-encrypt composition computes the MAC of the plaintext m, appends the MAC to the plaintext, and encrypts the resulting value:

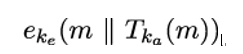
The MAC-then-encrypt composition is illustrated in Figure 15.2. This time, Alice first computes a MAC for plaintext m using the message authentication key ka and concatenates the plaintext with the MAC value she has just computed. Alice then encrypts the intermediate value m ∥ Tka(m) using the encryption key ke.

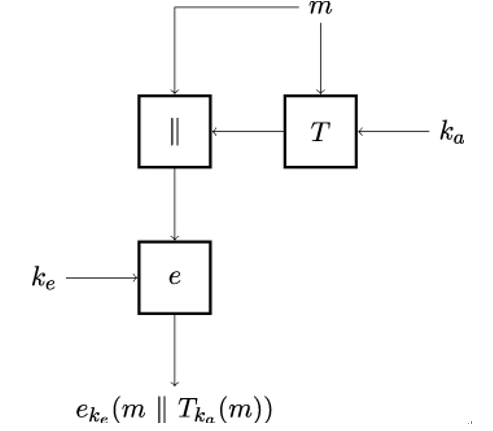
Figure 15.2: MAC-then-encrypt composition

Like with the other two compositions, encrypt-and-MAC and encrypt-then-MAC, the use of two distinct keys ke≠ka is a good practice in cryptographic mechanisms and cryptographic protocols to further increase their security level.

As we have already stressed in earlier chapters, the rationale behind this good practice is that even if Eve or Mallory were to somehow compromise one of the secret shared keys, the other key would remain intact. So, either the encryption or the message authentication would still work. In other words, the compromise of a single key does not lead to a complete compromise of the authenticated encryption mechanism.

Upon receiving Alice’s message, Bob decrypts it to obtain plaintext m and its corresponding MAC. Bob then computes the MAC for m using the shared secret key ka and verifies that the received MAC is equal to the computed MAC. If this is the case, he accepts the message as genuine.

Note that in the MAC-then-encrypt construction, the ciphertext is not protected by the MAC and can be modified by Mallory without being detected. This fact is used in so-called padding oracle attacks (see Chapter 19, Attacks on Cryptography).

15.2.3 Encrypt-then-MAC

The encrypt-then-MAC composition first encrypts the plaintext to obtain the ciphertext eke(m), then computes the MAC of the ciphertext, and finally appends the MAC value to the ciphertext:

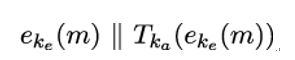
The encrypt-then-MAC composition is illustrated in Figure 15.3. First, sender Alice encrypts plaintext m using the shared encryption key ke. She then computes the MAC value for the ciphertext c = eke(m) using the message authentication key ka. Finally, Alice concatenates the ciphertext eke(m) with the MAC Tka(eke(m)).

After receiving Alice’s message, Bob takes the ciphertext c = eke(m) and computes the MAC for that ciphertext using key ka. He then compares the computed MAC with the received MAC. If the values are equal, Bob knows that the message was not manipulated and was sent by Alice. Hence, Bob proceeds by decrypting the ciphertext eke(m) using the shared encryption key ke. If the two MAC values do not agree, however, Bob will refrain from decryption as obviously there has been a transmission error or some other ciphertext manipulation.

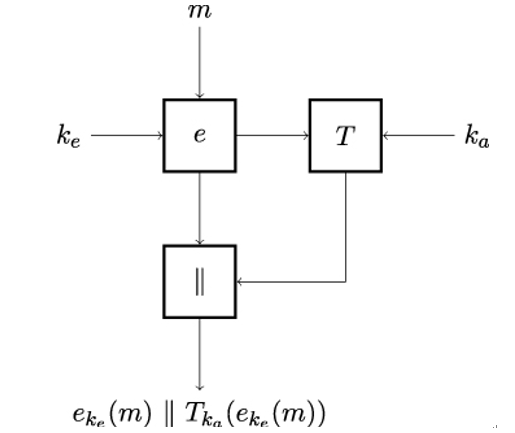
Figure 15.3: Encrypt-then-MAC composition

In the encrypt-then-MAC construction, the ciphertext is protected by the MAC. The encrypt-then-MAC construction therefore avoids the problem of modifiable ciphertext and may be viewed as the most secure way to do generic composition.