15.1 Preliminaries

Before diving into the details of authenticated encryption, we must first introduce some security concepts that we will need later on for an in-depth understanding and comparison of different authenticated encryption schemes.

15.1.1 Indistinguishability under a chosen-plaintext attack

Recall that our intuitive understanding of secure encryption is captured in the formal notion of indistinguishability in the presence of an eavesdropper. The key idea of indistinguishability is captured in the game – sometimes referred to as an experiment in cryptographic literature – played by Eve and some other party, let’s say, Owen:

1. Eve chooses a pair of equal-size messages m0,m1.
2. Owen generates a random secret key k and chooses a bit b ←{0,1} at random.
3. Owen then computes the ciphertext c = ek(mb) – referred to as the challenge ciphertext – and gives it to Eve. (Note that we use ek instead of fk here to denote encryption because the messages m0,m1 in this experiment can have a size different from that of a single plaintext block.)
4. Upon receiving c, Eve must guess whether b was 0 or 1. If Eve’s guess is correct, we say that Eve succeeds.

A secret key encryption is said to be indistinguishable in the presence of an eavesdropper if Eve succeeds in the above game with a probability P that is at most negligibly greater than 1 ∕ 2:

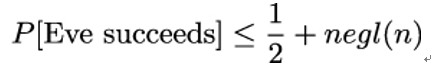
where negl(n) denotes a function that is negligible in the security parameter n. In Chapter 4, Encryption and Decryption, we already learned that a negligible function is a function that decreases faster toward zero with n than the reciprocal of any polynomial. The phrase security parameter is n means that the secret key k is an n-bit value k ←{0,1}n chosen uniformly at random.

CPA-secure is a stronger notion of security because a chosen-plaintext attack increases Eve’s capabilities. If Eve conducts a CPA, she can ask so-called encryption oracle Owen for encryption of multiple messages that she can choose adaptively. Essentially, Eve can freely interact with Owen – by providing him with a plaintext m as input and receiving the resulting ciphertext c = Ek(m) – before having to guess the value of bit b. The modified game now looks like this:

1. Owen generates a random secret key k.
2. Eve can freely interact with Owen, that is, she can ask Owen to compute the ciphertexts for any plaintexts of her choice.
3. Eve chooses a pair of equal-size messages m0,m1.
4. Owen chooses a bit b ←{0,1} at random and computes the challenge ciphertext c = Ek(mb).
5. Upon receiving c, Eve continues to have oracle access to Owen and must guess whether b was 0 or 1. If Eve’s guess is correct, we say that Eve succeeds.

Similar to the previous definition, a secret key encryption is said to be indistinguishable under a chosen-plaintext attack (IND-CPA) or, equivalently, CPA-secure, if Eve succeeds in the above game with a probability P that is at most negligibly greater than 1 ∕ 2:

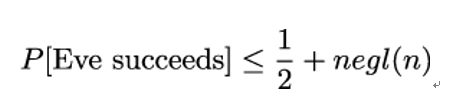
In other words, an encryption is CPA-secure if Eve cannot distinguish between the encryption of the messages m0,m1 even if she has access to an encryption oracle.

Note that Eve could easily succeed if the encryption ek was deterministic. In that case, all she has to do is to give Owen the messages m0,m1 and compare the corresponding ciphertexts c0,c1 to the challenge ciphertext. Consequently, to be CPA-secure, the encryption ek must be probabilistic [97]: it must use randomness during the computation of the ciphertext such that no two encryptions of the same plaintext (block) lead to the same ciphertext (block). Clearly, any encryption that is indistinguishable under a CPA is also indistinguishable in the presence of an eavesdropper.