16.1 Preliminaries

According to the American security researchers David McGrew and John Viega, ”the Galois/Counter Mode is a block cipher mode of operation that uses universal hashing over a binary Galois field to provide authenticated encryption [114].”

Before studying the internals of the algorithm, we need to quickly cover two mathematical aspects: the finite field used by GCM and the way multiplication is done in that finite field.

16.1.1 The Galois field 𝔽2128

GCM uses multiplication over a finite field. In mathematics, finite fields are also referred to as Galois fields in honor of the 19th-century French mathematician Evariste Galois, hence the name Galois counter mode.

We have already encountered finite fields in section 7.6 Finite Fields in Chapter 7, Public-Key Cryptography. You may go back to that section to refresh your memory, but we are repeating the basic facts here for your convenience.

The field used in GCM has 2128 elements, which are represented as polynomials of degree smaller than 128 with coefficients ∈{0,1}. As there are 128 binary coefficients, we get 2128 field elements.

In order to complete the definition of the field, we also need the field polynomial

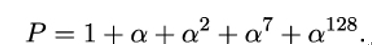
In the polynomial representation, the multiplication of two field elements X and Y is performed by multiplying the polynomial representing X with the polynomial representing Y and taking the result modulo P. This means we divide the 256-bit polynomial X ⋅Y by the field polynomial 1 + α + α2 + α7 + α128, and take the 128-bit remainder as the final result. Note that this remainder is a polynomial of degree less than 128 and therefore an element of our field.

To actually compute the multiplication of two finite field elements X and Y , they are treated as bit vectors and processed as shown in algorithm 4, which was given by McGrew and Viega in [114]. The i-th bit of element X is denoted as Xi, where the leftmost bit is X0 and the rightmost bit is X127. Then,

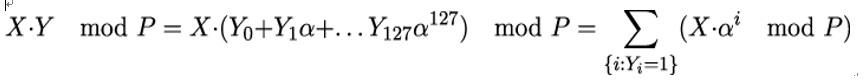
Algorithm 4 implements this formula by repeatedly multiplying X by α modulo P and adding up the results. For this, the multiplication algorithm uses a special field element R = 11100001 ∥ 0120. Its polynomial representation is

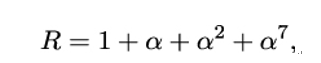
so it is equal to the field polynomial without the leading term.

The rightshift function shifts the bits of its argument cyclically by one bit to the right. It is the bitwise equivalent of multiplying X by α. On the other hand, R is chosen so that α ⋅ X ⊕ R resembles the polynomial (α ⋅ X) mod P. If X127 = 0; however, multiplication by α causes no wrap-around, and (α ⋅ X) mod P = (α ⋅ X).

  Algorithm 4: Multiplication of Field Elements ∈𝔽2128

Require: Elements X,Y ∈𝔽2128
 Ensure: Multiplication result Z = X · Y
 Z ← 0
 V ← X
 for i = 0 … 127 do
 if Y i = 1 then
 Z ← Z ⊕ V
 end if
 if V 127 = 0 then
 V ← rightshift(V ) else
 else
 V ← rightshift(V ) ⊕ R
 end if
 return Z

The addition of two field elements X, Y is simply the addition of two polynomials. Recall the coefficients of polynomials representing the field elements are in 𝔽2 = {0,1}. As a result, addition can be computed as X ⊕ Y . Moreover, subtraction is identical to addition in 𝔽2.